
H.-J. Euler, S. Seeger, F. Takac,
GNSS 2004 Proceedings Sydney, December 2004.
(Abstracts) (Hindsights) [Acrobat, 609KB]
Using the Master-Auxiliary concept, described in Euler et al. (2001), Euler and Zebhauser (2003) investigated the feasibility and benefits of standardized network corrections for rover applications. The analysis, focused primarily in the measurement domain, demonstrated that double difference phase errors could be significantly reduced using standardized network corrections.
Extended research investigated the potential of standardized network RTK messages for rover applications in the position domain (Euler et al, 2004-I). The results of baseline processing demonstrated effective, reliable and homogeneous ambiguity resolution performance for long baselines (>50km) and short observation periods (>45 sec). In general horizontal and vertical position accuracy also improved with the use of network corrections.
This paper concentrates on the impact of wrongly determined integers within the reference station network on RTK performance. A theoretical study using an idealized network of reference stations is complemented by an empirical analysis of adding incorrect L1 and L2 ambiguities to the observations of a real network. In addition, the benefits of using network RTK corrections for a small sized network in Asia during a period of high ionospheric activity is also demonstrated.
No hindsights yet.

H.-J. Euler, S. Seeger, O. Zelzer, F. Takac, B.E. Zebhauser,
ION GNSS 2004 Long Beach, September 2004.
(Abstracts) (Hindsights) [Acrobat, 861KB]
The current network RTK messages proposal, the so-called Master-Auxiliary concept, has been outlined in a number of publications (Euler et al., 2001 and Zebhauser et al., 2002). The messages describe the dispersive and non-dispersive errors for a network of reference stations. This information is normally interpolated for the rover’s position and applied to reduce the observation errors and improve positioning performance.
Euler et al. (2004) demonstrates the benefits of network RTK corrections in terms of positioning reliability, robustness and accuracy. The data used for the investigation was collected under fair atmospheric conditions. This paper concentrates on data collected during the severe ionospheric conditions recorded in October 2003. The advantage of network RTK information is measured in terms of the percentage of correctly fixed ambiguities.
The Master-Auxiliary concept, as with other network RTK methods, relies on the correct resolution of the integer ambiguities between the reference stations to model the dispersive and non-dispersive network errors. This paper also investigates the influence of incorrectly fixed reference station ambiguities on interpolated network RTK information. Two approximation surfaces are investigated: a linear plane and higher order surface represented by a quadratic function.
No hindsights yet.

H.-J. Euler, S. Seeger, O. Zelzer, F. Takac, B.E. Zebhauser,
ION NTM 2004 Proceedings San Diego, January 2004.
(Abstracts) (Hindsights) [Acrobat, 588KB]
A working group within RTCM SC104 for the standardization of network RTK messages has consolidated various message proposals put before the committee over the past 3 years and interoperability testing is currently underway. Therefore, an industry-wide network message standard is forthcoming.
Euler and Zebhauser (2003) and Euler et al. (2003) investigated the feasibility and benefits of standardized network corrections for rover applications. The Master-Auxiliary concept, described in Euler et al. (2001), as the network RTK message format. The analysis, focused primarily in the measurement domain, demonstrates that double difference phase errors can be significantly reduced using standardized network corrections.
This paper extends the analysis of standardized network RTK messages for rover applications to the position domain. The results of baseline processing demonstrate effective, reliable and homogeneous ambiguity resolution performance for long baselines (>50km) and short observation periods (>45 sec). Overall horizontal and vertical positional accuracy is also improved when network corrections are employed.
No hindsights yet.

M. Benz, X. Laboureux, T. Maier, N. Nkenke, S. Seeger, F.W. Neukam, G. Häusler,
In G. Greiner, H. Niemann, T. Ertl, B. Girod, H.-P. Seidel, Eds., Vision, Modeling and Visualization 2002 ISBN 3-89838-034-3 (Aka), Erlangen, 2002.
(Abstracts) (Hindsights) [Acrobat, 509KB]
In this paper we present an application of optical metrology and image processing to oral and maxillofacial surgery. Our goal is to support the surgeon intraoperatively during the repair of a displacement of the globe of the eye. To date, the surgeon has to evaluate his operation result solely by visual judgement. Our idea is to provide the surgeon intraoperatively with a comparison of the actual 3D position of the globe of the eye and its nominal position. The nominal position is computed based on symmetry considerations. Therefore, we have developed a method to compute the symmetry plane of faces in the presence of considerable asymmetry. We tested this method on healthy faces and on faces with a defined asymmetric region created by injection of saline solution.
No hindsights yet.

S. Seeger, G. Häusler,
Lehrstuhl für Optik, annual report 2001, page 35. Friedrich-Alexander-Universität Erlangen, 2002.
(Abstracts) (Hindsights) [Acrobat, 133KB]
In a previous report we introduced the concept of Selectively Refinable Progressive Meshes (SRPM) as the ideal data structure for complex numerical tasks. Meanwhile we finished the implementation of this data structure, provided a viewer for the visualization of the SRPM, and extended the idea of SRPMs in two ways: in dynamically loading the mesh we enable to work with arbitrarily large models, and in introducing the concept of subdivision quarks we allow to infinitely refine selected regions of interest.
No hindsights yet.
S. Seeger, X. Laboureux, G. Häusler,
Lehrstuhl für Optik, annual report 2001, page 32. Friedrich-Alexander-Universität Erlangen, 2002.
(Abstracts) (Hindsights) [Acrobat, 125KB]
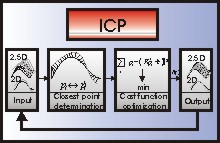
In a previous report we presented a comparison of Iterated Closest Point (ICP) algorithms. Now, a theoretical work regarding the localization accuracy of surfaces motivated the use of a new cost function for ICP algorithms. The comparison with a usual cost function shows that the new approach enables more robust results with significantly less computation time.
No hindsights yet.
A Sub-Atomic Subdivision Approach.
S. Seeger,
K. Hormann,
G. Häusler,
G. Greiner.
In B. Girod, H. Niemann, H.-P. Seidel, Eds.,
Vision, Modeling and Visualization 2001, pages 77-85.
Akademische Verlagsgesellschaft, Berlin, 2001.
(Abstracts)
(Hindsights)
[Acrobat, 388KB]
[Talk Slides, 4.64MB]
One of the main objectives of scientific work is the analysis
of complex phenomena in order to reveal the underlying structures
and to explain them by means of elementary rules which are easily
understood.
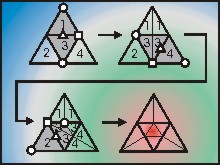
In this paper we study how the well-known process of triangle
mesh subdivision can be expressed in terms of the simplest
mesh modification, namely the vertex split.
Although this basic operation is capable of reproducing all
common subdivision schemes if applied in the correct manner,
we focus on Butterfly subdivision only for the purpose of
perspicuity.
Our observations lead to an obvious representation of subdivision
meshes as selectively refined progressive meshes, making them most
applicable to view-dependent level-of-detail rendering.
The second part of the paper
that describes the geometry of subdivision quarks is not any more
up-to-date. Meanwhile we developed and implemented a scheme that is even
more adaptive during successive subdivision than usual adaptive
subdivision schemes based on red-green triangulations. In
addition, the data structure of the selectively refinable progressive mesh has
been simplified. Probably, sub-atomic subdivision is therewith the most fundamental, most
general and simplest approach to adaptive subdivision that
is possible. The real-time on-the-fly generation of adaptive subdivision
meshes in a view-dependent level-of-detail system also proves the performance
of this approach.
S. Seeger,
Technical Report, Chair for Optics
(Abstracts) (Hindsights) [Acrobat, 205KB]
The basic idea of the registration approach we presented in A Robust Multiresolution Registration Approach is to calculate for each point in range image 1 the rotation and translation to each point in range image 2 with the help of their local frames and to store the resulting transformation parameters in a six dimensional Hough table by incrementing a counter in the table at position of the transformation parameters. Since transformations calculated from correct point correspondences result in the same transformation while all other transformations are distributed more or less randomly in the parameter space, a peak is expected in the Hough table at the position of the searched transformation.
Since the number of Hough table cells is limited due to limited memory resources, each Hough table cell has only a limited resolution that is connected to the size of the initial parameter domain. This Hough table cell resolution is far beyond the desired accuracy of the transformation determination when no or only little a priori knowledge is given for the initial parameter domain. The solution to this problem is to start with a rough resolution for each Hough table cell, detect the Hough peak so that the parameter domain can be restricted to the neighborhood of the peak, and then iterate the procedure by choosing each time a higher resolution for the Hough table cells.
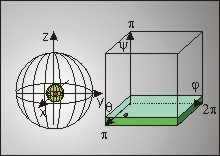
There are some practical problems in determining the neighborhood of the transformation that corresponds to the Hough peak. Since the topology of rotation parameters is non trivial (independent of the chosen parameterization) Hough cells that are far away from each other in the Hough table can be close to each other in the sense of corresponding rotations. A simple example is a rotation angle whose values 0 and 360 degrees are close to each other in the sense of rotations but far away in the Hough table since they lie on opposite sites of the table.
In this paper we examine the neighborhood structure for three rotation representations: the Euler angle representation, the axis and angle representation and the quaternion representation.
No hindsights yet.
S. Karbacher, S. Seeger, G. Häusler,
In Proceedings Third Int. Conf. on 3-D Digital Imaging amd Modeling, pages 270-277, IEEE Computer Society, Los Alamitos, 2001.
(Abstracts) (Hindsights) [Acrobat, 1.13MB]
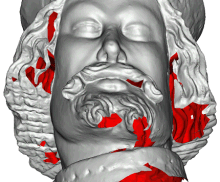
Subdivision schemes are commonly used to obtain dense or smooth data representations from sparse discrete data. E. g., B-splines are smooth curves or surfaces that can be constructed by infinite subdivision of a polyline or polygon mesh of control points. New vertices are computed by linear combinations of the initial control points. We present a new non-linear subdivision scheme for the refinement of triangle meshes that generates smooth surfaces with minimum curvature variations. It is based on a combination of edge splitting operations and interpolation by blending circular arcs. In contrast to most conventional methods, the final mesh density may be locally adapted to the structure of the mesh. As an application we demonstrate how this subdivision scheme can be used to reconstruct missing range data of incompletely digitized 3-D objects.
No hindsights yet.
S. Seeger, G. Häusler,
Lehrstuhl für Optik, annual report, page 16. Friedrich-Alexander-Universität Erlangen, 2001.
(Abstracts) (Hindsights) [Acrobat, 99KB]
Complex numerical tasks such as correlation problems in several dimensions, solving partial differential equations with lots of (spatial) boundary conditions or the visualization of highly detailed models with interactive control all face the same difficulty: The great amount of input data is too large to be handled in real-time. The only way to overcome this problem is to reduce the input data. Selectively refinable progressive meshes are in our eyes the ideal data structure to perform this task for surface data.
No hindsights yet.

S. Karbacher, S. Seeger, G. Häusler,
In B. Girod, H. Niemann, H.-P. Seidel, Eds., Vision, Modeling and Visualization 2000, pages 163-170. Akademische Verlagsgesellschaft, Berlin, 2000.
(Abstracts) (Hindsights) [Acrobat, 597KB]
Subdivision schemes are commonly used to obtain dense or smooth data representations from sparse discrete data. E. g., B-splines are smooth curves or surfaces that can be constructed by in- finite subdivision of a polyline or polygon mesh of control points. New vertices are computed by linear combinations of the initial control points. We present a new non-linear subdivision scheme for the refinement of triangle meshes that generates smooth surfaces with minimum curvature variations. It is based on a combination of edge splitting operations and interpolation by blending circular arcs. In contrast to most conventional methods the final mesh density may be locally adapted to the structure of the mesh. As an application we demonstrate how this subdivision scheme can be used to reconstruct missing range data of incompletely digitized 3-D objects.
No hindsights yet.

S. Seeger, X. Laboureux,
A long version of our book article in B. Girod, G. Greiner, and H. Niemann, Eds., Principles of 3D Image Analysis and Synthesis, pages 153-166, Kluwer Academic Publishers, Boston-Dordrecht-London, 2000.
(Abstracts) (Hindsights) [Acrobat, 363KB]
The purpose of this paper is to present a survey of rigid registration (also called matching) methods applicable to surface descriptions. As features are often used for the registration task, standard feature extraction approaches are described in addition. In order to give the reader a framework for his present registration problem, this report divides the matching task into three major parts (feature extraction, similarity metrics and search strategies). In each of them the reader has to decide between several possibilities, whose relations are in particularly pointed out.
In this overview we missed the important work of A.E. Johnson to Spin-Images.

B. Glomann, X. Laboureux, S. Seeger,
Lehrstuhl für Optik, annual report 1999, page 62. Friedrich-Alexander-Universität Erlangen, 2000.
(Abstracts) (Hindsights) [Acrobat, 111KB]
In order to digitize the surface of a complex object, several range images have to be taken from different viewpoints. To generate a complete model from these range images, in a first step all of them have to be transformed to the same coordinate system. In order to find the rotation and translation between two range images of overlapping surface regions - this process is called registration} - usually an Iterated-Closest-Points (ICP) algorithm is performed after a coarse alignment of the images has been given. Since the ICP algorithm allows much freedom in its implementation we compared several of such possibilities with respect to their accuracy and speed. All implementations based on triangle meshes as input data.
No hindsights yet.
Comparison of ICP-algorithms: First Results.
S. Seeger, X. Laboureux, B. Glomann,
Technical Report Chair for Optics, Friedrich-Alexander-Universität Erlangen, 2000.
(Abstracts) (Hindsights) [Acrobat, 78KB]
We present first interesting results based on the framework we introduced in our previous report A Framework for a Comparison of ICP-algorithms.
No hindsights yet.
A Framework for a Comparison of ICP-algorithms.
S. Seeger, X. Laboureux, B. Glomann,
Technical Report Chair for Optics, Friedrich-Alexander-Universität Erlangen, 2000.
(Abstracts) (Hindsights) [Acrobat, 73KB]
In order to digitize the surface of a complex object, several range images have to be taken from different viewpoints. To generate a complete model from these range images in a first step all of them have to be transformed to the same coordinate system. In order to find the rotation and translation between two range images of overlapping surface regions - this process is called registration - usually a variation of an Iterated-Closest-Point (ICP) algorithm is performed when a rough alignment of the images is already given. We developed a class library that allows the documentation of different ICP-algorithms and their - due to a common code basis - objective comparison with respect to their accuracy and speed.
No hindsights yet.
S. Seeger, G. Häusler,
In B. Girod, H. Niemann, H.-P. Seidel, Eds., Vision, Modeling and Visualization '99, pages 75-82, Infix Verlag, Sankt Augustin, Germany, 1999.
(Abstracts) (Hindsights) [Acrobat, 190KB] [Talk Slides, 1.07MB]
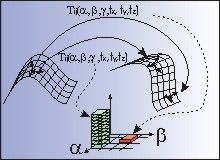
The task of registering several range images taken from different viewpoints into a single coordinate system is usually divided into two steps: first, finding a rough estimate of the searched transformation on the base of reduced parts of the data sets, and second, finding the precise transformation with another method on the base of the complete information given by the data sets. Using different approaches for these registration steps has no fundamental but only practical reasons: for the fine tuning step it exists an easily implementable algorithm whose efficiency and precision has been proven in many experiments, but which is not applicable for finding an initial rough estimate of the searched transformation. We present a multiresolution approach to the registration problem that has the potential to combine these two registration steps and is based on hierarchical Hough methods and local frames defined in each surface point.
No hindsights yet.
X. Laboureux, S. Seeger, G. Häusler,
Lehrstuhl für Optik, annual report 1998, page 52. Friedrich-Alexander-Universität Erlangen, 1999.
(Abstracts) (Hindsights) [Acrobat, 19KB]
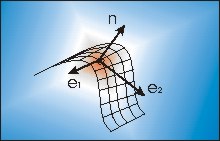
Curvatures are shift and rotation invariant local features of an object surface, well suited for object localization and recognition. Since they are very sensitive to noise (2nd order derivatives), a locally parametric surface description is a convenient way to smooth the noise. In this report we present how to calculate the extremal curvatures at each point of a parametric surface using partial derivatives with respect to the surface parameters. In a second step we show that the matrix used to determine the partial derivatives on 2.5D raster data is independent from the location within the image, which facilitates and speeds up the calculation of the curvatures.
No hindsights yet.

S. Seeger,
Technical Report, Lehrstuhl für Theoretische Kernphysik, Friedrich-Alexander-Universität Erlangen, 1995.
(Abstracts) (Hindsights) [Acrobat, 480KB]
No hindsights yet.

S. Seeger,
Diploma thesis, Friedrich-Alexander-Universität Erlangen, 1995.
(Abstracts) (Hindsights) [Acrobat, 624KB]
Die Quantenchromodynamik (QCD) ist die Theorie, von der man annimmt, dass sie die starke Wechselwirkung beschreibt. Bei dieser Theorie handelt es sich um eine Eichtheorie, in der - wie in jeder Eichtheorie - unterschiedliche Eichfeldkonfigurationen die gleiche Physik beschreiben, sodass eine Redundanz in der Anzahl von Freiheitsgraden in der Theorie vorliegt. Diese Redundanz kann dazu benutzt werden, einige Eichfelder durch eine sogenannte Eichfixierung zu eliminieren. Klassisch versteht man unter dieser Elimination das zu Null Setzen bestimmter Eichfreiheitsgrade. In der quantisierten Theorie ist jedoch zu beachten, dass es sich bei den Eichfeldern um Operatoren in einem Hilbertraum handelt, die nicht einfach in einer Operatoridentität gleich dem Nulloperator gesetzt werden können, da die kanonischen Kommutatorrelationen zwischen Eichfeldern und deren konjugierten Impulsen beachtet werden müssen. Unter der Elimination von Eichfreiheitsgraden versteht man hier einfach nur, dass die Symmetrie des Hamilton-Operators derart ausgenutzt wird, dass bestimmte Eichfreiheitsgrade durch Anwendung unitärer Transformationen nicht mehr im Hamilton-Operator auftreten.
Im Rahmen einer Hamiltonschen Formulierung der Theorie bietet es sich an - noch unmittelbar bevor man die Theorie durch Forderung kanonischer (Anti-)Kommutatorrelationen quantisiert -, in die sogenannte Weyl-Eichung überzugehen, in der auf klassischer Ebene die Null-Komponente des Eichfeldes zu Null gesetzt (A_0=0) wird (Dadurch werden Schwierigkeiten bei der kanonischen Quantisierung von A_0 - aufgrund des Fehlens der Zeitableitung von A_0 in der Lagrangedichte und dem daraus resultierenden Problem der Definition eines konjugierten Impulses zu A_0 - vermieden.). Da auf diese Weise die zu A_0 gehörige Euler-Lagrange-Gleichung - das Gaußche Gesetz - verloren geht, muss diese extra als eine Zwangsbedingung an physikalische Zustände gefordert werden: physikalische Zustände werden als Eigenzustände des Gauß-Gesetz-Operators - dieser ist als der nach Null aufgelöste Term der A_0-Euler-Lagrange-Gleichung in Operatorform erklärt - zum Eigenwert Null definiert.
Diese als Gauß-Gesetz bezeichnete Zwangsbedingung an physikalische Zustände ist insbesondere abhängig von den konjugierten Impulsen Pi der räumlichen Komponenten der Eichfelder A, die auch in der Weyl-Eichung noch eine Eichfreiheit aufweisen. Das Gauß-Gesetz kann nun dazu benutzt werden zu entscheiden, welche Eichfreiheitsgrade durch eine weitere Eichfixierung am vorteilhaftesten zu eliminieren sind. Das Kriterium bei dieser Entscheidung ist, nach welchen konjugierten Impulsen der Eichfelder sich das Gauß-Gesetz am leichtesten auflösen lässt. Denn wird eine Eichfixierung in den dazugehörigen Eichfreiheitsgraden vorgenommen, d.h. werden diese Eichfreiheitsgrade durch eine unitäre Transformation aus dem Hamilton-Operator eliminiert, so kann mit Hilfe des Gauß-Gesetzes ein im physikalischen Sektor gültiger Ausdruck für die konjugierten Impulse dieser Eichfreiheitsgrade gefunden werden, sodass diese ebenfalls im Hamilton-Operator des physikalischen Sektors nicht mehr auftreten. Erst durch die Elimination von Eichfreiheitsgraden mitsamt den dazugehörigen konjugierten Impulsen aus dem Hamilton-Operator des physikalischen Sektors wird in konsistenter Weise eine Eichfixierung durchgeführt.
Das Auflösen des Gauß-Gesetzes nach konjugierten Impulsen irgendwelcher Eichfreiheitsgrade ist in jedem Fall mit der Invertierung eines Operators verbunden. Wie man sich am einfachsten in der Eigenbasis dieses Operators klar macht - dort kann man den Operator in seiner Wirkung auf einen Basisvektor durch den dazugehörigen Eigenwert ersetzen -, treten Probleme bei der Operatorinvertierung genau dort auf, wo der Operator verschwindene Eigenwerte besitzt. Die bei der Invertierung resultierenden Singularitäten bei verschwindenen Eigenwerten bezeichnet man als Infrarotsingularitäten (In Anlehnung an die bei Entwicklungen üblich benutzte Basis von ebenen Wellen (Fouriertransformation!), in der Wellenzahlvektoren k als Eigenwerte eines Impulsoperators auftreten und verschwindene Eigenwerte somit großen Wellenlängen (infrarot) entsprechen.). Um diesen Infrarotschwierigkeiten in wohldefinierter Weise zu begegnen, muss man die Null-Eigenwerte aus dem (kontinuierlichen) Spektrum isolieren, um sie dann in gesonderter Weise zu behandeln. Die erforderliche Diskretisierung des Spektrums wird dadurch erreicht, dass man von dem zu invertierenden Operator, welcher sich in der 3+1 dimensionalen Theorie als x-abhängig erweist, fordert, dass er periodischen Randbedingungen unterliegt (Damit sollten auch die Eigenzustände periodischen Randbedingungen unterliegen, was zur Diskretisierung des Spektrums führt.). Diese Periodizität wird automatisch erfüllt, wenn die Theorie in der Weyl-Eichung von vornherein auf einem Torus formuliert wird (d.h. wenn von vornherein für die Eichfelder periodische Randbedingungen und für die Massefelder quasiperiodische Randbedingungen gefordert werden). Man formuliert die Theorie also auf einem Torus, um Infrarotschwierigkeiten geeignet zu begegnen.
Wie bereits erwähnt, werden am vorteilhaftesten diejenigen Eichfreiheitsgrade durch die Eichfixierung eliminiert, nach deren konjugierten Impulsen sich das Gauß-Gesetz am einfachsten auflösen lässt. Ob die Auflösung des Gauß-Gesetzes nach konjugierten Impulsen der gerade betrachteten Eichfreiheitsgrade nun einfach ist oder nicht, lässt sich auf formaler Ebene an dieser Stelle noch nicht entscheiden, da die Auflösung des Gauß-Gesetzes nur mit der (formalen) Invertierung eines Operators verbunden ist (Formal lässt sich das Inverse eines Operators O einfach als O^-1 schreiben.). Will man die Invertierung jedoch explizit machen, so muss man in die Eigenbasis des zu invertierenden Operators übergehen, um den Operator in seiner Wirkung auf Basisvektoren durch Zahlen (Eigenwerte) ersetzen zu können. Dafür muss notwendigerweise das Eigenwert-Problem des zu invertierenden Operators gelöst werden. Mit der einfachen Auflösung des (transformierten) Gauß-Gesetzes ist daher gemeint, dass das Eigenwert-Problem des mit dieser Auflösung verbundenen Operators einfach, d.h. analytisch lösbar ist.
Auf dieses Kriterium hin können nun die üblich verwendeten Eichbedingungen untersucht werden. Die Lorentz-Eichbedingung kommt von vornherein nicht in Frage, da wir durch Verwendung des Hamiltonschen Formalismus und der Weyl-Eichung uns schon gegen eine kovariante Eichung entschieden haben. Bei der Coulomb-Eichung, in der der longitudinale Anteil des Eichfeldes aus dem Hamilton-Operator eliminiert wird, ist in der 3+1 dimensionalen QCD mit der Auflösung des Gauß-Gesetzes nach dem longitudinalen Anteil des konjugierten Impulses die Invertierung eines Operators verbunden, dessen Eigenwert-Problem nicht analytisch gelöst werden kann. Einzig in der Axialen Eichung, in der die 3-Komponente des Eichfeldes aus dem Hamilton-Operator eliminiert wird, ist der zu invertierende Operator mit einem analytisch lösbaren Eigenwert-Problem verknüpft.
Es bietet sich also an, die QCD im Hamiltonschen Formalismus in der Weyl-Eichung auf einem Torus zu formulieren und die weitere Eichfixierung in der Axialen Eichung durchzuführen. Nun zeigt sich jedoch, dass die Formulierung auf dem Torus die vollständige Elimination der 3-Komponente des Eichfeldes aus dem Hamilton-Operator verhindert. In einer Arbeit von Lenz et al. wird daher in einem ersten Schritt zunächst soviel von der 3-Komponente des Eichfeldes durch eine unitäre Transformation aus dem Hamilton-Operator eliminiert, wie mit einer Formulierung auf dem Torus verträglich ist. In einem zweiten Schritt wird dann ein niederdimensionales Feld in den 1,2-Komponenten des Eichfeldes aus dem Hamilton-Operator entfernt. Dieses Vorgehen bei der Eichfixierung werden wir der Einfachheit halber als Axiale Eichung bezeichnen. In einer von Palumbo vorgeschlagenen klassischen Eichbedingung, die von M.Thies in den quantenmechanischen Formalismus der Eichfixierung übertragen wurde, wird alternativ in einem ersten Schritt nur soviel von der 3-Komponente des Eichfeldes eliminiert, wie im schwachen Kopplungslimes mit der Auflösung des Gauß-Gesetzes nach dem zugehörigen konjugierten Impuls verträglich ist. Man erwartet daher, dass die sogen. Palumbo-Eichung insbesondere für den schwachen Kopplungslimes geeignet ist. In einem 2. und 3. Schritt der Eichfixierung werden dann niederdimensionale Felder in der 2- und 1-Komponente des Eichfeldes - in völliger formaler Analogie zum ersten Schritt der Eichfixierung - aus dem Hamilton-Operator eliminiert.
Sowohl in der Palumbo-Eichung als auch in der Axialen Eichung verbleiben nach der Eichfixierung globale, d.h. x-unabhängige Rest-Gauß-Gesetze in der Theorie, die nicht mehr durch Auflösung nach konjugierten Impulsen in den Hamilton-Operator implementiert werden, da eine weitere Auflösung formal sehr aufwendig wird. Diese Rest-Gauß-Gesetze definieren die physikalischen Zustände nach den unitären Eichfixierungstransformationen.
Im Rahmen dieser Arbeit sollen nun Axiale und Palumbo-Eichung in einer Raum- und einer Zeitdimension (1+1 dim) vergleichend dargestellt werden. In 1+1-Dimensionen ist die Eichung bereits nach der ersten unitären Transformation fixiert. Dies führt dazu, dass die Palumbo-Eichung sich von der Axialen Eichung nur dadurch unterscheidet, dass sie nicht so weit fixiert wurde wie die Axiale Eichung. Einen neuen Namen (nämlich Palumbo-Eichung) für die nicht so weit fixierte Axiale Eichung einzuführen, erscheint eigentlich nicht gerechtfertigt und ist nur vom Standpunkt der 3+1 dimensionalen Theorie zu verstehen.
Innerhalb einer Approximation wollen wir in der 1+1 dimensionalen Theorie eine alternative Methode zur Eichfixierung mittels unitärer Transformationen vorstellen. Auf diese Weise werden wir die Hamilton-Operatoren der Axialen und der Palumbo-Eichung ineinander überführen.
In Arbeiten von B.Schreiber und M.Engelhardt wurde gezeigt, dass in der 1+1 dimensionalen QCD durch die sorgfältige Betrachtung der Theorie auf dem endlichen Intervall eine partielle Rechtfertigung für das Farbdogma des nichtrelativistischen Quarkmodells möglich ist. Dieses Farbdogma besagt, dass Quarks in realisierten Zuständen stets zum Farbsingulett abgekoppelt werden. Der Rest der Wellenfunktion (Ort, Spin, Flavor) ist dann wegen des Pauliprinzips symmetrisch unter Austausch der Quarks.
Die Rechtfertigung des Farbdogmas folgte insbesondere aus der detaillierten Untersuchung des Spektrums des eichfixierten Hamilton-Operators in der Approximation statischer, d.h. unendlich schwerer Quarks. Bei Schreiber wurde dieses Spektrum auf analytische Weise exakt bestimmt. Wir wollen zeigen, wie man diese exakten Resultate bereits in einer Störungsrechnung in L erhalten kann, wobei L der Umfang des Kreises ist, auf dem man die Theorie formuliert.
Die Arbeit ist folgendermaßen gegliedert.
Im 2.Kapitel werden wir ausgehend vom Weyl-Hamilton-Operator der 1+1 dimensionalen QCD die eichfixierten Hamilton-Operatoren der Axialen und der Palumbo-Eichung für eine SU(N)-Theorie ableiten. Dieses Kapitel dient uns in erster Linie zur Einführung in die verwendeten Bezeichnungen und Größen.
Im 3.Kapitel beschäftigen wir uns mit der kinetischen Energie der Nullmoden in Axialer und Palumbo-Eichung. Wir referieren die auf die 1+1 dimensionale QCD übertragenen Ergebnisse von Lenz für die Axiale Eichung und übertragen die beschriebene Vorgehensweise auf die Palumbo-Eichung.
Im 4.Kapitel spezialisieren wir die Theorie auf den statischen Limes der 1+1 dimensionalen QCD mit einer SU(2)-Farbgruppe und für baryonische Zustände. In der Axialen Eichung konstruieren wir zunächst nach dem Vorbild von Schreiber die physikalischen Baryonzustände und übertragen das Konstruktionsprinzip anschließend auf die Palumbo-Eichung. Abschließend werden wir in Störungsrechnung 1.Ordnung in L das Spektrum des vollständig eichfixierten Hamilton-Operators in der beschriebenen Approximation bestimmen.
Im 5.Kapitel werden die Ergebnisse zusammengefasst und diskutiert.
No hindsights yet.